(Public domain video)
Chapter 6 Guided Practice Problems
6.1 Complications with Process Costing
6.1.1 It Starts Innocently Enough
In Chapter 4, I made a parenthetical comment about dividing overhead evenly between individual product units. When product units are relatively homogeneous (i.e. not customized, not given a job name, not given an order number), it probably isn’t worthwhile to apply overhead costs to each item as if it’s uniquely responsible for a different amount of overhead costs. If all the product units are the same, each product unit is probably responsible for the same amount of overhead cost. To spend time or money on deciding each unit’s responsibility for overhead costs down to the micro-penny is a waste.
This leads to process costing, which tries to allocate actual overhead costs equally across homogeneous individual product units.
Why “process” costing? When each individual product unit is the same, managers are not going to spend time thinking about individual product units—they’re all the same! Instead they spend time thinking about and trying to improve the processes that spit out those individual product units.
Appropriately, then, process costing pools costs at the process-level (which usually means its pooled at the department-level) rather than being pooled at the job-level or the unit-level.
In its simplest form, process costing applies overhead cost to each product unit: total actual overhead cost divided by total units gives overhead cost per unit. There’s no need to develop a budgeted PDOH rate beforehand, as there is in job-order costing. So, this calculation can take place after the close of the period. In that case process costing rates are almost like “post-determined overhead rates.”
NOTE: Do not use this equation for process costing calculations. It ignores key complications discussed below. It is shown for narrative purposes only.
While this is indeed the basic structure of process costing, there are three big complications.
6.1.2 Complication #1: Units in Ending WIP Inventory
For many process costing firms, there are units still in process when the month or quarter or year ends. Some overhead cost should go to these units still in WIP, just not a full unit’s worth of overhead costs. These units probably aren’t responsible for the same amount of overhead that fully complete units are.
How much overhead do they deserve? That depends on how complete they are. If the process is constantly being repeated across homogeneous units, then we can consider a unit’s percent completion as an indicator of how much of the process’s overhead costs that unit has incurred.
Process costing firms don’t use units in the denominator (that is, of the overhead per cost equation given above). Instead they use equivalent units (sometimes called equivalent units of production). Each product unit is scaled by its percent completion. (Firms examine what’s left unfinished at the end of the period to come up with those units’ “percent completion.”)
I phrase this equation in the singular (i.e. “unit”), but process costing firms usually calculate equivalent units for groups of units, rather than for individual units. The implicit assumption is that all units in the group are roughly at the average same level of completion (process costing firms are very unlikely to find it useful to get more specific than that).
So, for example, in the same way that a single unit that is 40% complete equals 0.4 equivalent units (1 * 0.4 = 0.4), a group of 500 units that are 40% complete equals 200 equivalent units (500 * 0.4 = 200).
By using equivalent units, process costing firms still account for completed product units as whole units, while allowing
This leads to the very-important term total equivalent units (which I will sometimes abbreviate as TEU). To assign costs, process costing firms only need to calculate equivalent units for (1) the units still in ending WIP and (2) the units completed. Thus sum of these equivalent units is the total equivalent units they need for their cost allocations (the below equation does change slightly under the FIFO method,
Notice that I simply wrote “Completed Units” instead of the technically correct “Completed Units * percent completion” because, by definition, completed units are always 100% complete. In other words, units equals equivalent units when we’re talking about completed units.
Let’s update our overhead allocation equation to incorporate our first complication of equivalent units.
NOTE: Do not use this equation for process costing calculations. It ignores key complications discussed below. It is shown for narrative purposes only.
The overhead cost per unit number has now transformed into an overhead cost per equivalent unit number. To reiterate, this allows the overhead cost we allocated to ending WIP units to be scaled by those ending WIP units’ percent completion.
For example, let’s say we calculate a cost of $5 per equivalent unit. If ending WIP has 200 units that are 50% complete, that equals 100 equivalent units. These 200 units would be allocated $500 in cost (i.e. $5 cost per equivalent unit * 100 equivalent units = $500 cost allocated). This seems fitting: this allocation is exactly 50% of the cost these 200 units would have been allocated if we hadn’t scaled ending WIP by percent completion (i.e. 200 units * $5 = $1,000, which would overvalue ending WIP).
6.1.3 Complication #2: Non-uniform Consumption of Product Costs
There are two parts to this complication. First, product costs (meaning direct materials, direct labor, and overhead). Process costing firms usually find it inefficient to trace any costs to individual product units, including costs that are traditionally considered direct materials or direct labor. It just doesn’t make sense to track how many milliseconds each worker spends on each product unit among a sea of identical product units moving down an assembly line.
So when these firms allocate overhead, they also allocate direct materials and direct labor, i.e. all product costs.
That means all product costs need to be put into the numerator of a cost per equivalent unit calculation. Our equation starts to look like this.
NOTE: Do not use this equation for process costing calculations. It ignores a key complication discussed below. It is shown for narrative purposes only.
The second part of this complication is non-uniform consumption. That might sound like meaningless jargon, but it’s name is actually pretty logical. I’ll walk you through it.
The actual manufacturing process used in process costing firms usually isn’t uniform. Specifically, direct material costs are rarely incurred at the same time as labor and overhead costs.
In a common scenario, all direct materials costs are incurred at the beginning of the process. For example, a bunch of sheet metal is placed in a machine (which then converts the sheet metal into the finished product). Or, a block of wood is placed on the assembly line (where worked then convert it into the finished product). Labor and overhead costs, in these examples, are incurred only after there’s a piece of metal in the machine or a block of wood on the assembly line to work on. We call the sum of labor and overhead conversion costs because they are costs incurred to convert raw materials into finished goods.
In short, these are common examples where 100% of direct materials are added at the beginning of the process. Thus it would be appropriate for process costing to reflect 100% of direct material cost being incurred at the beginning of the process.
Let’s assume a unit in ending WIP is about halfway through the process of completion. Halfway painted, halfway baked, halfway polished. Whatever. It would be natural to assume it is about 50% complete (and thus equal to 0.5 equivalent units).
However this unit probably may already have most if not all of its direct materials, i.e. ~100% complete with respect to direct materials. 100% of the wood that needs to be painted, 100% of the clay that needs to be baked, or 100% of the metal that needs to be polished is already on the assembly line. It might be 50% complete with respect to the conversion process that transforms those raw materials into finished products. But it is not 50% complete with respect to the direct materials themselves.
Direct materials can also be incurred elsewhere in the process. Let’s say your department cooks dumplings (a prior department prepared the dumplings; your job is just to cook them).
Here’s the process.
(1) Get a pot of water out (equipment and water costs are likely overhead).
(2) Apply heat (heating costs are likely overhead as well).
(3) Not watch the pot (haha!).
(4) Add the dumplings (i.e. direct materials) to boiling water.
(5) Cook the dumplings until delicious.
(6) Give the dumplings to me.
The direct materials aren’t used until midway through the process.
Here’s another example, if you are a printing company. You probably do some consulting (i.e. labor and overhead) with the customer before sending the job to the printer. Notice that direct materials (i.e. the paper and ink) are not applied until toward the end of the process.
As a result of the fact that the percent completion of direct materials often does not match the percent completion of conversion costs, process costing firms will calculate two separate cost-per-equivalent-unit numbers: one for direct materials per equivalent unit and the other for conversion costs per equivalent unit.
6.1.4 Complication #3: Transfers between Departments
Process costing firms usually have several departments that products must pass through before they’re complete. For responsibility accounting purposes these departments costs should be kept separate. So each department allocates costs at the end of the period to reflect the units that department completed and transferred onward to the next department.
(For convenience, I’m going to use the term department and process interchangeably, since department divisions usually approximate the divisions between different processes.)
That is, they input a journal entry between two departmental WIP accounts. Each department will have it’s own WIP account If a firm uses three different departments (e.g. mixing, assembly, and packaging), then it will also have three different WIP accounts (i.e. WIP-mixing, WIP-assembly, and WIP-packaging).
Notice that this matches what I said earlier: process costing firms pool costs at the department-level. Whereas job-order costing firms usually have separate WIP accounts for each job (since jobs are the focus of management’s attention), process costing firms usually have a separate WIP account for each department, since processes are the focus of management’s attention.
When Department A is done with some product units and passes those units onward to Department B, then we credit the WIP-A account for the cost of those units and debit the WIP-B account for the cost of those units.
Department B then treats this cost as a transferred-in cost. Often it creates a separate per-equivalent-unit equation for transferred in costs. (Thus the first department in the process wouldn’t have transferred-in costs.)
If this seems daunting, just remember that the percent completion for transferred-in costs is always 100%. Transferred-in costs are incurred in a different department during a process completed by that department. If those costs weren’t 100% complete, the product wouldn’t have been transferred out of that department! If you recognize this, you can simplify your transferred-in cost calculations somewhat.
6.2 Putting it All Together
6.2.1 Overview of Process Costing
Now that we’ve talked about the complications that make process costing the way it is, let’s look at the process costing cycle.
At the beginning of the period, each department has a debit balance for the cost of any units in beginning WIP. Then, throughout the current period, the department incurs more costs that are debited to WIP.
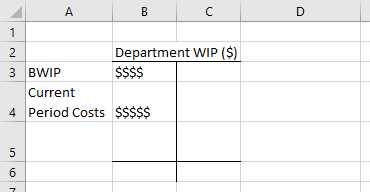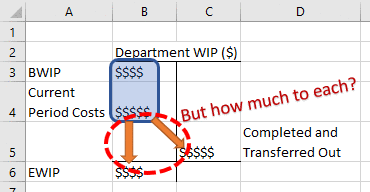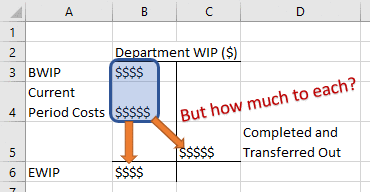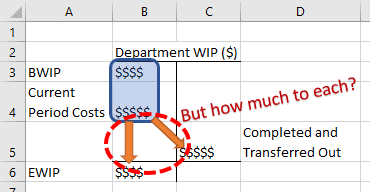
The overall objective of process costing is to take these costs and redistribute them between (1) ending WIP and (2) the credit side of the WIP account (i.e. completed and transferred out costs).
At the end of the period, the firm determines ending WIP percent completion and determines units completed. Then the firm engages the following cycle to determine where the costs go.
- STEP #1 Calculate total equivalent units. You need a separate total equivalent units number for direct materials, conversion costs, and (if applicable) transferred-in costs.
- STEP #2 Calculate cost-per-equivalent-unit rates. You need a separate rate for direct materials, conversion costs, and (if applicable) transferred-in costs.
- STEP #3 Multiply Step 2 rates by (1) ending WIP equivalent units and (2) completed and transferred out units. Do this within each cost category (e.g. direct material rate multiplied by direct materials equivalent units).
After these steps, you’ve answered the question in the animation above: how much cost goes to goods completed and transferred out and how much goes to ending WIP.
6.2.2 A Tale of Two Methods
There are two methods for completing these steps: weighted average and first-in, first-out (i.e. FIFO). These two methods differ in how they treat beginning WIP. (So, by extension, if there are zero beginning WIP units, then the two methods provide the same results.)
The weighted average method lumps in beginning WIP costs with current period costs. It treats the last-period work that beginning WIP costs represents as if it were done this period. FIFO keeps beginning WIP costs separate, building a special carpool lane for them to move directly to the credit side of the WIP account. This (1) ensures these costs are “first-out” since they were literally the “first-in” at 12:00 am of the first day of the period, and (2) it makes sure that work from last period does not affect this period’s rates (I’ll elaborate on this second point later).
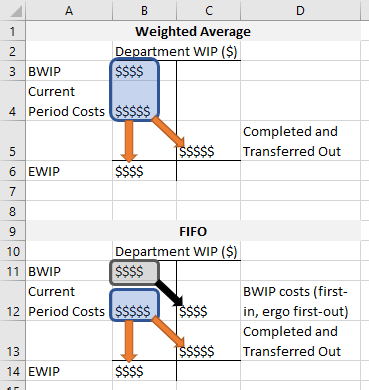
This has several ripple effects. As we saw in Sections 6.1.3 and 6.1.4, cost per equivalent unit rates (see Step 2 above) come in three varieties as follows. (Do use these equations!)
Weighted average and FIFO differ in how they define the six terms on the left-hand side of these equations. It’s a small difference, but I’ve seen it trip up lots of people.
- If a firm uses weighted average, these six terms include beginning WIP costs (for numerators) and beginning WIP equivalent units (for denominators).
- If the firm uses the FIFO method, these terms do not include beginning WIP costs (for numerators) and beginning WIP equivalent units (for denominators).
6.3 Equivalent Units Calculations (STEP #1)
6.3.1 Weighted Average Equivalent Units (STEP #1)
In Section 6.1.2, I defined total equivalent units as the sum of equivalent units at the destination of the orange arrows: (1) ending WIP units and (2) units completed and transferred out. This is technically only the weighted average version of the equation (we’ll talk about the FIFO version below).
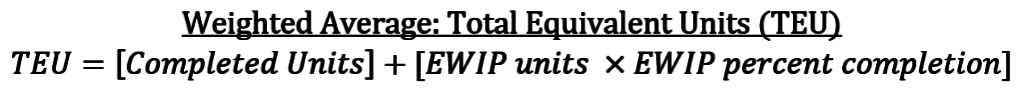
I’ve put these terms in brackets for illustrative purposes (I know they’re not required for order of operations purposes). Each bracketed section reflects an orange arrow in my illustration.
NOTE: Units completed, completed units, and units completed and transferred out are interchangeable terms that all mean the same thing.
The weighted average firm just doesn’t care that some “completed units” are actually beginning WIP units that already had some work done on them last period. Instead the weighted average method completely detaches beginning WIP costs from partially-complete beginning WIP units. Beginning WIP units get lumped in with all “Completed Units” as if they had no work at all done last period.
So, for example, let’s assume the following facts for a department.
- 100 units in beginning WIP (50% complete with respect to conversion costs).
- Starts 1,000 units this period.
- 200 units in ending WIP (40% complete with respect to conversion costs).
- All materials (direct materials and transferred-in materials) are added at the beginning of the process.
- This department is the second in the production chain.
First, you have to tease out units completed. Let’s do this by creating a “unit T-account.”
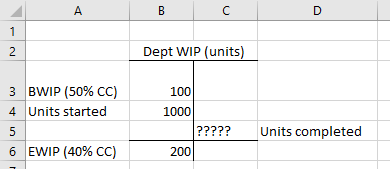
The firm completed 900 units (100 BWIP units + 1,000 units started – 200 EWIP units = 900 units completed). Total equivalent units (i.e. TEU) for our three process costing categories would be calculated as follows.
- DM TEU: 900 + 200 * 1.00 = 1,100 (Remember, all materials are added at the beginning of the process, so all ending WIP units are 100% completed with respect to materials.)
- CC TEU: 900 + 200 * 0.40 = 980
- TI TEU: 900 + 200 * 1.00 = 1,100 (Just like DM, all materials are added at the beginning of the process.)
We’ll use these total equivalent units numbers in the denominator to calculate cost rates.
6.3.2 FIFO Equivalent Units (STEP #1)
The FIFO version of the total equivalent units equation starts from the weighted average equation but subtracts out the beginning WIP equivalent units. This is because are trying to calculate the total equivalent units of work completed this period, and beginning WIP equivalent units represent work done last period.
Let’s rearrange this equation a little.
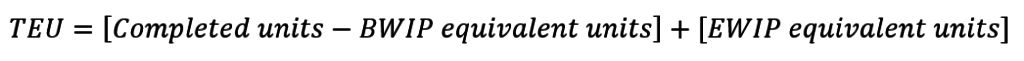
The first term in the brackets is important. That’s what FIFO considers completed units: only the work done this period. At the end of the process costing cycle, a FIFO firm will apply this period’s rates to only that first bracketed term.
Let’s look at the FIFO/weighted average illustration again.
The bracketed term helps scale the FIFO rate to the diagonal orange arrows. For FIFO the “Completed and Transferred Out” cell above doesn’t include work done last period, i.e. the work represented by beginning WIP costs in the gray box. Those last-period, beginning WIP costs move directly along the black arrow to the credit side of the T-account. They were costs tied to units that were first-in (as in, those units were started before 12:00am at the beginning of the period, so you can’t get earlier than that). Therefore, those costs by rule follow the beginning WIP units they are tied to, which are assumed to be the first units completed.
Using the same example from the weighted average method, let’s use the following facts.
- 100 units in beginning WIP (50% complete with respect to conversion costs).
- Starts 1,000 units this period.
- 200 units in ending WIP (40% complete with respect to conversion costs).
- All materials (direct materials and transferred-in materials) are added at the beginning of the process.
- This department is the second in the production chain.
Again, the firm must have completed 900 units. The total equivalent units (i.e. TEU) for our three process costing categories are calculated as follows.
DM TEU: 900 + 200 * 1.00 – 100 * 1.00 = 1,000
CC TEU: 900 + 200 * 0.40 – 100 * 0.50 = 930
TI TEU: 900 + 200 * 1.00 – 100 * 1.00 = 1,000
Compare these numbers to the weighted average numbers from earlier. Each total equivalent units figure is smaller using FIFO. This is always the case when there are beginning WIP equivalent units. If there are no beginning WIP units, the two methods operate in exactly the same way. Again, the only difference between the two methods is that stinking beginning WIP.
6.4 Weighted Average Rates and Cost Allocation (STEP #2 and STEP #3)
6.4.1 Weighted Average Rates (STEP #2)
This section covers Steps 2 and 3 from our overview of process costing: calculate cost per equivalent rates and then use those rates to allocate costs between completed units and ending WIP.
First, let’s review our rate equations.
We already covered how the weighted average and FIFO methods define the denominators differently. Now let’s talk about their differences in defining numerators. For the weighted average method, you add beginning balances to current period costs.
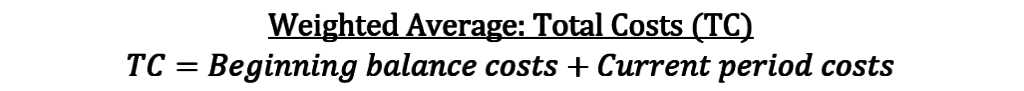
Here’s an example of the
- A firm completes 20,000 units this period.
- The firm has 500 units left in ending WIP that are 40% complete with respect to conversion costs.
- At the end of
last period, 600 units were still unfinished. These units are 60% complete with respect to conversion costs. - The beginning balance for conversion costs is $15,000
- Current period conversion costs are $300,000.
Conversion cost per equivalent unit, then, is $15.59 ([$300,000 + $15,000] / [20,000 * 1 + 500 * 0.4]).
The weighted average method rips away the $15,000 of conversion costs from the beginning WIP units. It treats those $15,000 as if they were incurred this period (even though we know they were incurred last period, otherwise they wouldn’t be the beginning WIP balance). This means those $15,000 of conversion costs end up redistributed across all equivalent units worked on this period because they’re included in the conversion cost per equivalent unit rate we just calculated. The units in beginning WIP are effectively treated as if they had no work done on them at all in the prior period, and they are lumped in with all the other units completed this period.
What makes this method a “weighted average” is that p
If the firm frequently has significant swings in per-unit costs, the weighted average method is less appropriate. It holds workers and managers accountable, in part, for cost decisions from
6.4.2 Weighted Average Cost Allocation (STEP #3)
For the weighted average method, applying costs is relatively simple. You apply costs by multiplying the rates for direct materials, conversion costs, and transferred-in cost by (1) ending WIP equivalent units and (2) completed units.
To be clear this means six separate multiplications.
- DM rate * DM EWIP equivalent units
- CC rate * CC EWIP equivalent units
- TI rate * TI EWIP equivalent units
- DM rate * DM completed units
- CC rate * CC completed units
- TI rate * TI completed units
Under the weighted average method, “completed units” will be the same for all costing types: direct materials, conversion costs, and transferred-in costs. You can combine those last three multiplication steps into one single step. This cannot always be done for FIFO, as explained below.
If you sum the three ending WIP products above, you have the total cost of ending WIP. If you sum the three units completed products above, you have the total cost of units completed and transferred out.
Hey look, those are the numbers we’ve been looking for this whole time! (It’s always in the last place you look.)
Why go through all this trouble?
Well, ending WIP cost is important
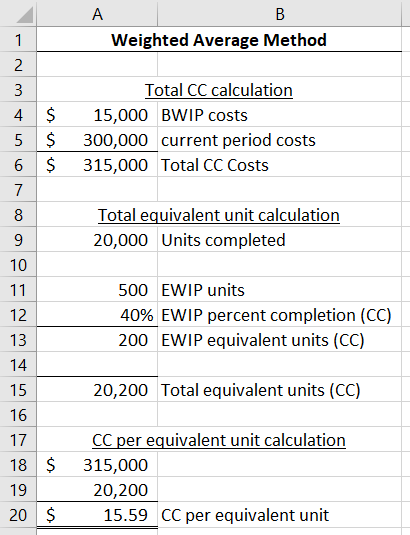
Below, I continue with the above example to allocating costs. I assume materials are added at the beginning of the process, so ending WIP units are 100% complete with respect to direct materials and transferred-in costs.
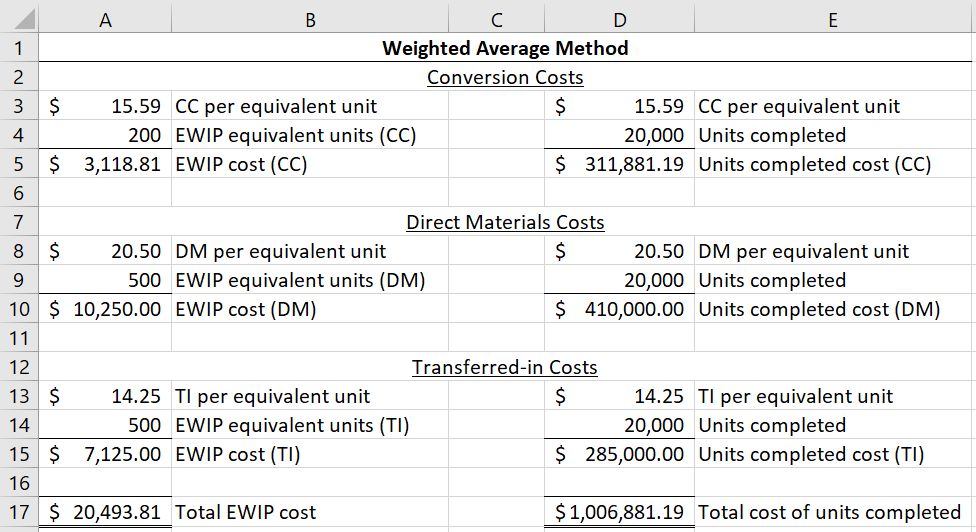
This leads to $1,006,881.19 credited to this department’s WIP account. That amount is either debited to the next department’s WIP account or to finished goods (if this is the last department in the production chain).
Even though the firm needs an aggregate number to get overall ending WIP value, the firm will want to keep data on how much of that $20,493.81 is due to conversion costs, direct materials, and transferred-in costs. That’s because this cycle will start again next period, and the firm will need to know how much beginning WIP costs are direct materials, conversion cost, and transferred-in costs for next period’s cost calculations.
6.5 FIFO Rates and Cost Allocation (STEP #2 and STEP #3)
6.5.1 FIFO Rates (STEP#2)
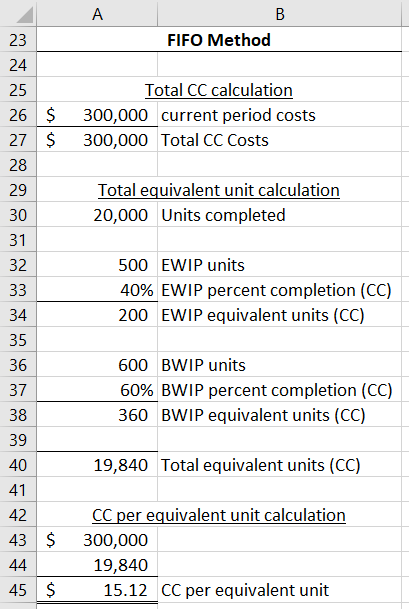
Under the FIFO
Let’s use the same numbers as the weighted average example. Assume the following.
- A firm completes 20,000 units this period.
- The firm has 500 units left in ending WIP that are 40% complete with respect to conversion costs.
- At the end of
last period, 600 units were still unfinished. These units are 60% complete with respect to conversion costs. - The beginning balance for conversion costs is $15,000.
- Current period conversion costs are $300,000.
Under FIFO, total conversion costs are only the $300,000 incurred this period. You do not include the $15,000 in beginning WIP (since those dollars will pass through directly to the cost of completed units). The denominator is 19,840 equivalent units ([20,000 * 1 + 500 * 0.4 – 600 * 0.6]).
Therefore, conversion cost per equivalent unit under the FIFO method is $15.12.
6.5.2 FIFO Cost Allocation (STEP #3)
If you are using FIFO, the procedure to allocate costs follows the same basic procedure as the weighted average method, with two differences: (1) FIFO uses a different idea of “completed units” that get this period’s rates and (2) FIFO uses an extra step that directly adds beginning WIP costs to the cost of units completed and transferred out.
Below I complete the same cost allocation example as with the weighted average method, but now with FIFO. I again assume materials are added at the beginning of the process, so ending WIP units are 100% complete with respect to direct materials and transferred-in costs.
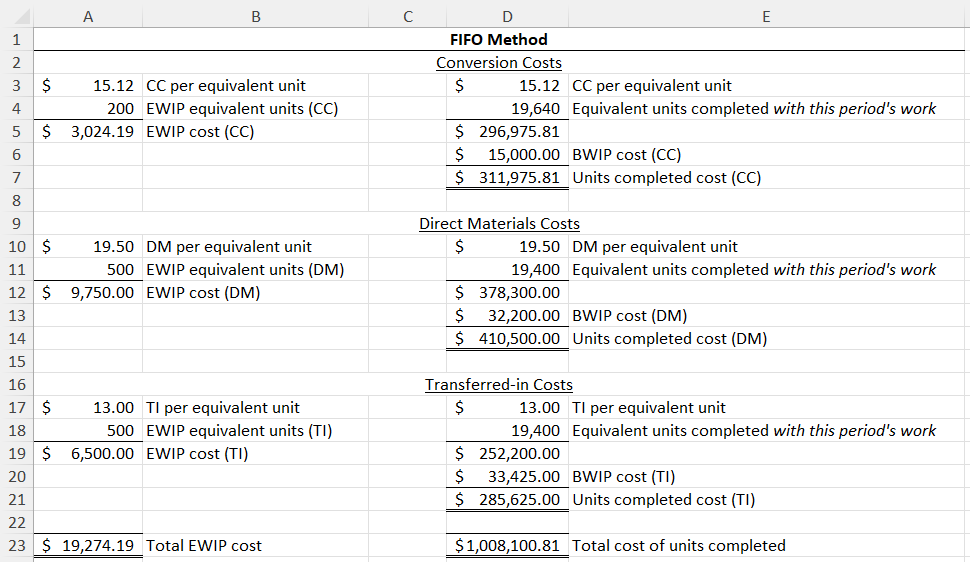
First, FIFO only applies this period‘s rate to work done this period. Beginning WIP is units that were partially completed last period. So, the beginning WIP equivalent units are subtracted away in order to arrive at “Equivalent units completed with this period’s work” (see cells E4, E11, and E18). That removes the portion of beginning WIP units that were completed last period.
Notably, “equivalent units completed with this period’s work” is calculated the same as in the first set of brackets below.
FIFO recognizes that the work represented by beginning WIP equivalent units wasn’t completed this period, so you wouldn’t apply this period’s cost rates to those equivalent units.
Second, the extra step. The extra step is to directly add beginning WIP cost to the units completed (see cells D6, D13, and D20 in the above figure). This is the black arrow in the FIFO diagram.
And now we’re done. What a process!
6.5.3 FIFO Step #3: Alternative Explanation (Additive Method)
I explained, above, FIFO’s Step #3 using what’s called the subtractive method. I told you to subtract the beginning WIP equivalent units from the total units completed so we could apply the rates to the equivalent units completed using this period’s work.
But this can be taught a different way too, called the additive method. Both methods produce the same final results. Also, the methods only differ in how they arrive at the cost of units completed and transferred out. Calculating the cost of ending WIP is always the same: multiply cost-per-equivalent-unit rates by equivalent units in ending WIP.
Textbooks that use the additive method introduce the term “Units started and completed.” This means units that were started and completed during this period. It excludes any units we started last period and completed this period (i.e. beginning WIP units) and any units we started this period but did not complete by the end of the period (i.e. ending WIP units). We only want those that were (1) started after 12:00 am on the first day of the period and (2) completed before 11:59 pm on the last day of the period.
The Units Completed term we’ve used already excludes any ending WIP units, so we just need to subtract away those units in beginning WIP.
Units Started and Completed = Units completed – BWIP units
Under FIFO, the Units Started and Completed definitely get this period’s rates. So that’s the first step: multiple Units Started and Completed by this period’s rates.
But Units Started and Completed were all started after 12:00 am, meaning they were not the “first-in.” We also need to include the first-in units (i.e. beginning WIP) in the units completed and transferred out.
But what is the cost of beginning WIP units? Well it has two parts: the cost of last period’s and the cost of this period’s work.
We had to “top off” the beginning WIP units this period to complete them. And that top-off belongs to this period and gets this period’s rates. The work done last period os reflected by beginning WIP costs. So the cost of beginning WIP, the first-in and first-out portion of the units completed and transferred out is reflected below.
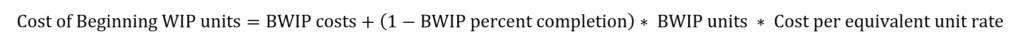
So, as a brief example of this calculation, if there were 100 beginning WIP units that were 40% complete with respect to conversion costs and carried $500 of conversion costs into the beginning WIP balance, that means we had to do 60% of their work this period to complete them. Assuming a rate of $6 per equivalent unit.
Conversion Cost of Beginning WIP units = $500 + (1 – 0.4) * 100 * $6
Conversion Cost of Beginning WIP units = $500 + 60 * $6
Conversion Cost of Beginning WIP units = $500 + 360 = $860
Add that $860 to whatever we figured was the conversion cost of Units Started and Completed and we have the total conversion costs of units completed and transferred out.
Compare the subtractive method (see above figure in Section 6.5.2) to the additive method (below).
